
 | Five Beginner and Intermediate Kakuro Solving Strategies |
If you are a Kakuro player, then you know that it can be quite a challenging type of puzzle if not harder than Sudoku. The object of the puzzle is to fill the white boxes with the correct digits that add up to the sum listed in the triangular box. For example, a row of three blocks with a sum of 10 on the end could be 1-2-7, 1-4-5, or several patterns of numbers.
There are a few key rules in playing:
 There are no zeroes in the puzzle only 1 to 9.
There are no zeroes in the puzzle only 1 to 9.
 No digit is repeated within any sum group.
No digit is repeated within any sum group.
 The order for a string of numbers may vary.
The order for a string of numbers may vary.
(ex. For a sum of 6, you may use:
1-2-3, 1-3-2, 2-3-1, 2-1-3, 3-1-2, or 3-2-1).
 There is only one unique and correct solution to a given puzzle.
There is only one unique and correct solution to a given puzzle.
There are a few key rules in playing:
(ex. For a sum of 6, you may use:
1-2-3, 1-3-2, 2-3-1, 2-1-3, 3-1-2, or 3-2-1).
 |
Like sudoku, there are many techniques in solving a kakuro puzzle. When the simple techniques don't work, you will need to use a more complicated solving technique. This can get to a point where it almost looks impossible to solve and may take a long time using a variety of strategies. But keep in mind, in a Kakuro puzzle there is only one unique solution that will work successfully. In this article I will give you a few kakuro strategies and will use the term rows for the across boxes and column for the down boxes.
Strategy #1: Common Numbers
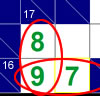
If a row has a sum of 16 over 2 squares and a column has a sum of 17 over 2 squares, the only possible values are 7-9 for the row and 8-9 for the column. Therefore, the only common value for the intersecting box is a 9. This strategy is best when starting off a puzzle.
Strategy #2: Use Pencil marks
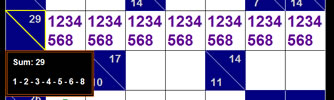
Although it may take extra work, using pencil marks not only greatly reduce the chance for error, it helps to point out obvious hints in solving puzzles. Now, it seems like I am stating the obvious but it very easy to overlook it and think "I got it, it is no big deal" only to run into a problem later on. Using pencil marks, it is best to fill in possible values that you know are going to exist in a particular box. You don't need to over do it sometimes but it is good for a small range. Then, as more clues are revealed, you can reduce the pencil marks until only one digit remain and that will be the digit used for that box.
*** Using pencilmarks will come in handy especially for the medium and hard levels. ***
Strategy #3: Pairs, Triples, Quadruples
This is a very good strategy when using pencil-marks. It is also a common strategy in Sudoku. The idea is to identify lone pairs, triples, and quadruples in a given row (or column) and eliminate those digits from the other boxes.
In Example A: if a box of a given row (or column) only has a pencil mark of (1,5) and another box in the same row (or column) also has a pencil mark of (1,5) then you can remove 1 and 5 from all other boxes in that row. The reason behind this is that the first box must be a 1 or a 5 and the second box must be a 1 or a 5. If the 3rd box was set as a 5 for example, it would cause an obvious error in the row since you are not allowed to have the same digit in a row or column.
In Example B: we have something known as a "Hidden Pair". Since (1,5) are only in box #2 and box #5 and (1,5) are not in any other boxes, then you can eliminate 2,3,4 from those two boxes. Example B can also be called a Triple since (2,3,4) are in 3 of the 5 boxes and therefore cannot be in the 2 boxes that also contain the (1,5). Depends on how you look at it, is the glass half full or half empty?
Strategy #4: Combo Elimination / Common Digits Within Sums
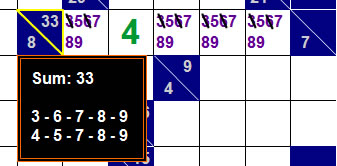
This strategy used is how you can further eliminate pencil marks. First, you make a list of all the combos that would add up to a given sum. Then you can eliminate combos based on the digits you already have filled in. For Example, a 5 digit sum of 33 is either a 3-6-7-8-9 or 4-5-7-8-9. Now if you already know that one of the boxes is a 4 (due to the 7 over 3 lets say...) then you know the other 4 boxes will contain a 5-7-8-9 not a 3-6-7-8-9, thus permanently eliminating 3 and 6 from any box in the row.
Another strategy that needs to be considered is that you notice the 2 sums that add up to 33: 3-6-7-8-9 or 4-5-7-8-9. Well, they both have 3 common digits 7-8-9. That means there MUST be a 7, 8, and 9 in that row... while the other 2 will either be a 3-6 or 4-5 (if you didn't have that green 4 already there). You can use this knowledge when combining other strategies like triples or hidden triples in this example.
Strategy #5: Testing Pencil-mark in Different Situations
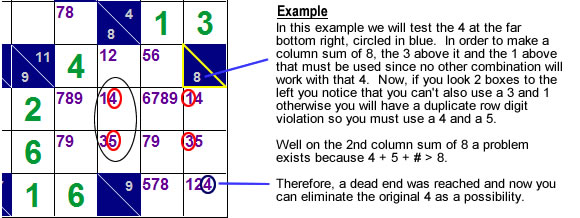
This can fall under a more advanced technique but is in fact an excellent way of removing pencil-mark digits. It is using different situations that will lead to a dead end and then removing the pencil-mark that lead to that dead end. You can think of it like, what would happen if this box was a 4? will it lead to a dead end somewhere else close to it? The example below describes such a situation:
Good luck on your next Kakuro puzzle!! (Click Here to Play)
Strategy #1: Common Numbers
If a row has a sum of 16 over 2 squares and a column has a sum of 17 over 2 squares, the only possible values are 7-9 for the row and 8-9 for the column. Therefore, the only common value for the intersecting box is a 9. This strategy is best when starting off a puzzle.
| Example |
 |
Strategy #2: Use Pencil marks
Although it may take extra work, using pencil marks not only greatly reduce the chance for error, it helps to point out obvious hints in solving puzzles. Now, it seems like I am stating the obvious but it very easy to overlook it and think "I got it, it is no big deal" only to run into a problem later on. Using pencil marks, it is best to fill in possible values that you know are going to exist in a particular box. You don't need to over do it sometimes but it is good for a small range. Then, as more clues are revealed, you can reduce the pencil marks until only one digit remain and that will be the digit used for that box.
*** Using pencilmarks will come in handy especially for the medium and hard levels. ***
| Example |
 |
Strategy #3: Pairs, Triples, Quadruples
This is a very good strategy when using pencil-marks. It is also a common strategy in Sudoku. The idea is to identify lone pairs, triples, and quadruples in a given row (or column) and eliminate those digits from the other boxes.
In Example A: if a box of a given row (or column) only has a pencil mark of (1,5) and another box in the same row (or column) also has a pencil mark of (1,5) then you can remove 1 and 5 from all other boxes in that row. The reason behind this is that the first box must be a 1 or a 5 and the second box must be a 1 or a 5. If the 3rd box was set as a 5 for example, it would cause an obvious error in the row since you are not allowed to have the same digit in a row or column.
| Example A - of a Pair: |
 |
In Example B: we have something known as a "Hidden Pair". Since (1,5) are only in box #2 and box #5 and (1,5) are not in any other boxes, then you can eliminate 2,3,4 from those two boxes. Example B can also be called a Triple since (2,3,4) are in 3 of the 5 boxes and therefore cannot be in the 2 boxes that also contain the (1,5). Depends on how you look at it, is the glass half full or half empty?
| Example B - of a Hidden Pair: |
 |
Strategy #4: Combo Elimination / Common Digits Within Sums
This strategy used is how you can further eliminate pencil marks. First, you make a list of all the combos that would add up to a given sum. Then you can eliminate combos based on the digits you already have filled in. For Example, a 5 digit sum of 33 is either a 3-6-7-8-9 or 4-5-7-8-9. Now if you already know that one of the boxes is a 4 (due to the 7 over 3 lets say...) then you know the other 4 boxes will contain a 5-7-8-9 not a 3-6-7-8-9, thus permanently eliminating 3 and 6 from any box in the row.
Another strategy that needs to be considered is that you notice the 2 sums that add up to 33: 3-6-7-8-9 or 4-5-7-8-9. Well, they both have 3 common digits 7-8-9. That means there MUST be a 7, 8, and 9 in that row... while the other 2 will either be a 3-6 or 4-5 (if you didn't have that green 4 already there). You can use this knowledge when combining other strategies like triples or hidden triples in this example.
| Example |
 |
Strategy #5: Testing Pencil-mark in Different Situations
This can fall under a more advanced technique but is in fact an excellent way of removing pencil-mark digits. It is using different situations that will lead to a dead end and then removing the pencil-mark that lead to that dead end. You can think of it like, what would happen if this box was a 4? will it lead to a dead end somewhere else close to it? The example below describes such a situation:
 |
Good luck on your next Kakuro puzzle!! (Click Here to Play)
| Your Feedback | |
| 02/28/2017 - Good tips. When I have to start trial and error, it feels like a cop out. Is there a way to avoid that? Was trying to compare sums of columns and rows, but that can get difficult depending on the puzzle configuration. Nice web site - Gary 07/07/2013 - It was ok - Marylynn 04/22/2009 - On Sunday or Monday, a box popped up to enter the number of a particular puzzle. Thats the first time that has happened, and I can figure out how I got it.Also, is there a way to access the answers? I believe that would be a learning tool if all else fails.Your puzzles are my on-line favorites. - Carolyn |